AC Voltage Applied to a Resistor

A $15.0$ $\text{μF}$  capacitor is connected to $220$ $\text{V,}$ $50$ $\text{Hz}$ source. The capacitive reactance and the RMS current would be:

An a.c. source, of voltage $V=V_m \sin \omega t$, is applied across a series LCR circuit. Which of the following is the phasor diagram for the circuit when capacitative impedance exceeds the inductive impedance?

A resistor of  $200\Omega$  and a capacitor of 15.0 $\text{μF}$  are connected in series to a 220 V, 50 Hz a.c. source. Calculate

​(i) The current in the circuit.

(ii) The rms voltage across the resistor and the capacitor.

The instantaneous current and voltage of an a.c. circuit are given by $I=10\sin 300t \mathrm{A}$ and $V=200\sin 300t \mathrm{V}$. What is the power dissipation in the circuit?

In a series LCR circuit, the voltage across an inductor, capacitor and resistor are $20 \mathrm{V}$, $20 \mathrm{V}$ and $40 \mathrm{V}$ respectively. What is the phase difference between the applied voltage and the current in the circuit?

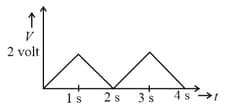
The RMS value of voltage of the waveform shown below is, $v_{rms}=\frac{k}{\sqrt{3}} \mathrm{V}$, find the value of $k$.

Chose the correct phasor diagram for a purely resistive a.c. circuit.

The graph between the current in a purely resistive a.c circuit and the alternating voltage applied is a_____.

Which graph represents the true resistive a.c. circuit?

Discuss a purely resistive circuit.

If a capacitor of $8\mathrm{ }\mathrm{\mu F}$ is connected to a $220\mathrm{ }\mathrm{V},\mathrm{ }100 \mathrm{H}\mathrm{z}$, AC source and the current passing through it is $65 \mathrm{m}\mathrm{A}$ then the rms voltage across it is

Assertion : The alternating current lags behind the e.m.f. by a phase angle of $\frac{\pi }{2}$, when AC flows through an inductor.
Reason : The inductive reactance increases as the frequency of AC source decreases.

Assertion: In a purely resistive ac circuit instantaneous power varies sinusoidally.

Reason: Applied ac voltage varies sinusoidally.

A sinusoidal voltage $v=200\sin 314t$ is applied to a resistor of $10\Omega$ resistance. Calculate the power dissipated as heat in $\mathrm{watt}$.

A sinusoidal voltage $v=200\sin 314t$ is applied to a resistor of $10\Omega$ resistance. Calculate the frequency of the supply.

The r-m-s value of AC voltage$V$ in terms of $\sin x$ and $\cos x$ is always same for a complete cycle.

The r-m-s value of $V_1=V_p \sin \left(\omega t\right)$ and $V_2=V_p \cos \left(\omega t\right)$ is _____ times $V_p$ for a complete cycle. Here, $V_p$ is peak voltage.

Compare the r-m-s value of $V_1=V_p \sin \left(\omega t\right)$ and $V_2=V_p \cos \left(\omega t\right)$ for a complete cycle. Here, $V_p$ is peak voltage.

The average value of $\cos x$ for the interval $\left[0,\frac{\mathrm{\pi }}{2}\right]$ is _____.

Find the average of the given function for the interval $0$ to $\frac{\mathrm{\pi }}{2}$.

$f\left(x\right)=\cos x$